ESTATÍSTICA INFERENCIAL
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 306.)
Um levantamento da Time/CNN solicitou a 814 adultos que respondessem a uma série de questões sobre suas perspectivas em relação à situação financeira dos Estados Unidos. Um total de 562 adultos respondeu Sim à questão: Você acha que as coisas estão indo bem nos Estados Unidos de hoje? (Time, 11 de agosto de 1997). Qual o intervalo de confiança de 90% para a proporção da população de adultos que sentem que as coisas estão indo bem nos Estados Unidos? Faça os cálculos com seis casas decimais e arredonde a resposta final para duas casas decimais.
Dados adicionais:
Z = 1,645.

69,04% ± 1,56%.
69,04% ± 4,13%.
69,04% ± 2,67%.
69,04% ± 3,72%.
69,04% ± 3,65%.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 344.)
No último ano o número de almoços servidos na cantina de uma escola de ensino fundamental foi distribuído normalmente com uma média de 300 almoços por dia. No início do corrente ano, o preço de um almoço foi aumentado em 25 centavos. Uma amostra de seis dias duramente os meses de setembro, outubro e novembro forneceu o número de crianças que efetivamente almoçaram: 290, 275, 310, 260, 270 e 275. Estes dados indicam que o número médio de almoços por dia tenha caído desde o último ano? Assinale a alternativa que indica as hipóteses nula (Ho) e alternativa (Ha) adequadas para testar se o número médio de almoços caiu desde o último ano.
Ho: µ ≥ 300 e Ha: µ < 300
Ho: µ < 300 e Ha: µ ≥ 300
Ho: µ ≠ 300 e Ha: µ = 300
Ho: µ = 300 e Ha: µ ≠ 300
Ho: µ ≤ 300 e Ha: µ > 300
Ao pesquisar a preferência dos consumidores para cinco marcas de cerveja em lata, um estudante de administração, estagiário em uma empresa especializada em marketing, estimou a média dos consumidores da marca S com a confiança de 95%, a partir de uma amostra de 27 entrevistados. O estudante sabia que a a população de consumidores de cerveja segue uma distribuição normal de probabilidades. Como o desvio padrão da população era desconhecido, o estagiário calculou o desvio padrão amostral. Para calcular a margem de erro, o estagiário usou a a distribuição normal padronizada Z, extraindo da tabela Z = 1,96. A respeito do acerto na escolha da distribuição de probabilidades usada pelo estudante, assinale a alternativa correta.
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido e a amostra é grande, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O estagiário errou ao escolher a distribuição de probabilidades Z. Dado que o desvio padrão populacional é desconhecido e a amostra é pequena, deveria ter usado a distribuição t, de Student, na construção do intervalo de confiança.
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido, mas a população de onde provém a amostra é normal, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido e a amostra é pequena, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O procedimento do estagiário está correto. Como a amostra provém de uma população normal, é indiferente o uso da distribuição normal padronizada Z ou da distribuição t, de Student.
Uma nova série de televisão precisa provar que tem mais do que 25% da audiência de telespectadores depois das 13 primeiras semanas de exibição para ser julgada bem sucedida. Quais as hipóteses nula (Ho) e alternativa (Ha) adequadas para testar se a série tem mais do que 25% da audiência de telespectadores depois das 13 primeiras semanas de exibição?
Ho: p ≥ 0,25 e Ha: p < 0,25
Ho: p = 0,25 e Ha: p ≠ 0,25
Ho: p ≤ 0,25 e Ha: p > 0,25
Ho: p > 0,25 e Ha: p ≤ 0,25
Ho: p ≠ 0,25 e Ha: p = 0,25
Considere o seguinte teste de hipóteses:
Ho: µ ≥ 25
Ha: µ < 25
Uma amostra com 100 elementos é extraída da população e fornece a média igual a 22 e o desvio padrão igual a 12. Para alfa igual a 5%, qual sua conclusão?
Dados adicionais:
Valor de Zcrítico = - 1,645.
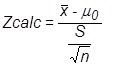
Não rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula porque Zcalc = 3,5 é maior que Z crítico.
Não rejeitar a hipótese nula, porque Zcalc = 2,5 é maior que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 3,5, é menor que Z crítico.
ENADE 2006 Adaptado.
A tabela abaixo mostra como se distribui o tipo de ocupação dos jovens de 16 a 24 anos que trabalham em 5 Regiões Metropolitanas e no Distrito Federal.

Das regiões estudadas, aquela que apresenta o maior percentual de jovens com carteira assinada, dentre os jovens que são assalariados do setor privado, é
Belo Horizonte.
Recife.
Porto Alegre.
Distrito Federal.
São Paulo.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 1,23%
± 5,23%
± 2,23%
± 4,23%
± 3,23%
O controlador de qualidade de certa empresa, desejando estimar a porcentagem de defeitos da linha de produção do produto A, examinou uma amostra de 1000 peças e encontrou 30 defeituosas. Com uma confiança de 95%, qual a porcentagem de peças defeituosas da linha de produção do produto A? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z = 1,96.

3,0%±3,36%.
3,0%± 0,05%.
3,0%±2,54%.
3,0%±2,84%.
3,0%±1,06%.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:

69,04% ± 1,56%.
69,04% ± 4,13%.
69,04% ± 2,67%.
69,04% ± 3,72%.
69,04% ± 3,65%.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 344.)
No último ano o número de almoços servidos na cantina de uma escola de ensino fundamental foi distribuído normalmente com uma média de 300 almoços por dia. No início do corrente ano, o preço de um almoço foi aumentado em 25 centavos. Uma amostra de seis dias duramente os meses de setembro, outubro e novembro forneceu o número de crianças que efetivamente almoçaram: 290, 275, 310, 260, 270 e 275. Estes dados indicam que o número médio de almoços por dia tenha caído desde o último ano? Assinale a alternativa que indica as hipóteses nula (Ho) e alternativa (Ha) adequadas para testar se o número médio de almoços caiu desde o último ano.
Ho: µ ≥ 300 e Ha: µ < 300
Ho: µ < 300 e Ha: µ ≥ 300
Ho: µ ≠ 300 e Ha: µ = 300
Ho: µ = 300 e Ha: µ ≠ 300
Ho: µ ≤ 300 e Ha: µ > 300
Ao pesquisar a preferência dos consumidores para cinco marcas de cerveja em lata, um estudante de administração, estagiário em uma empresa especializada em marketing, estimou a média dos consumidores da marca S com a confiança de 95%, a partir de uma amostra de 27 entrevistados. O estudante sabia que a a população de consumidores de cerveja segue uma distribuição normal de probabilidades. Como o desvio padrão da população era desconhecido, o estagiário calculou o desvio padrão amostral. Para calcular a margem de erro, o estagiário usou a a distribuição normal padronizada Z, extraindo da tabela Z = 1,96. A respeito do acerto na escolha da distribuição de probabilidades usada pelo estudante, assinale a alternativa correta.
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido e a amostra é grande, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O estagiário errou ao escolher a distribuição de probabilidades Z. Dado que o desvio padrão populacional é desconhecido e a amostra é pequena, deveria ter usado a distribuição t, de Student, na construção do intervalo de confiança.
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido, mas a população de onde provém a amostra é normal, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido e a amostra é pequena, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O procedimento do estagiário está correto. Como a amostra provém de uma população normal, é indiferente o uso da distribuição normal padronizada Z ou da distribuição t, de Student.
Uma nova série de televisão precisa provar que tem mais do que 25% da audiência de telespectadores depois das 13 primeiras semanas de exibição para ser julgada bem sucedida. Quais as hipóteses nula (Ho) e alternativa (Ha) adequadas para testar se a série tem mais do que 25% da audiência de telespectadores depois das 13 primeiras semanas de exibição?
Ho: p ≥ 0,25 e Ha: p < 0,25
Ho: p = 0,25 e Ha: p ≠ 0,25
Ho: p ≤ 0,25 e Ha: p > 0,25
Ho: p > 0,25 e Ha: p ≤ 0,25
Ho: p ≠ 0,25 e Ha: p = 0,25
Considere o seguinte teste de hipóteses:
Ho: µ ≥ 25
Ha: µ < 25
Uma amostra com 100 elementos é extraída da população e fornece a média igual a 22 e o desvio padrão igual a 12. Para alfa igual a 5%, qual sua conclusão?
Dados adicionais:
Valor de Zcrítico = - 1,645.
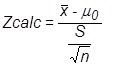
Não rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula porque Zcalc = 3,5 é maior que Z crítico.
Não rejeitar a hipótese nula, porque Zcalc = 2,5 é maior que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 3,5, é menor que Z crítico.
ENADE 2006 Adaptado.
A tabela abaixo mostra como se distribui o tipo de ocupação dos jovens de 16 a 24 anos que trabalham em 5 Regiões Metropolitanas e no Distrito Federal.

Das regiões estudadas, aquela que apresenta o maior percentual de jovens com carteira assinada, dentre os jovens que são assalariados do setor privado, é
Belo Horizonte.
Recife.
Porto Alegre.
Distrito Federal.
São Paulo.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 1,23%
± 5,23%
± 2,23%
± 4,23%
± 3,23%
O controlador de qualidade de certa empresa, desejando estimar a porcentagem de defeitos da linha de produção do produto A, examinou uma amostra de 1000 peças e encontrou 30 defeituosas. Com uma confiança de 95%, qual a porcentagem de peças defeituosas da linha de produção do produto A? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z = 1,96.

3,0%±3,36%.
3,0%± 0,05%.
3,0%±2,54%.
3,0%±2,84%.
3,0%±1,06%.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
Ho: µ ≥ 300 e Ha: µ < 300
Ho: µ < 300 e Ha: µ ≥ 300
Ho: µ ≠ 300 e Ha: µ = 300
Ho: µ = 300 e Ha: µ ≠ 300
Ho: µ ≤ 300 e Ha: µ > 300
Ao pesquisar a preferência dos consumidores para cinco marcas de cerveja em lata, um estudante de administração, estagiário em uma empresa especializada em marketing, estimou a média dos consumidores da marca S com a confiança de 95%, a partir de uma amostra de 27 entrevistados. O estudante sabia que a a população de consumidores de cerveja segue uma distribuição normal de probabilidades. Como o desvio padrão da população era desconhecido, o estagiário calculou o desvio padrão amostral. Para calcular a margem de erro, o estagiário usou a a distribuição normal padronizada Z, extraindo da tabela Z = 1,96. A respeito do acerto na escolha da distribuição de probabilidades usada pelo estudante, assinale a alternativa correta.
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido e a amostra é grande, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O estagiário errou ao escolher a distribuição de probabilidades Z. Dado que o desvio padrão populacional é desconhecido e a amostra é pequena, deveria ter usado a distribuição t, de Student, na construção do intervalo de confiança.
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido, mas a população de onde provém a amostra é normal, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido e a amostra é pequena, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O procedimento do estagiário está correto. Como a amostra provém de uma população normal, é indiferente o uso da distribuição normal padronizada Z ou da distribuição t, de Student.
Uma nova série de televisão precisa provar que tem mais do que 25% da audiência de telespectadores depois das 13 primeiras semanas de exibição para ser julgada bem sucedida. Quais as hipóteses nula (Ho) e alternativa (Ha) adequadas para testar se a série tem mais do que 25% da audiência de telespectadores depois das 13 primeiras semanas de exibição?
Ho: p ≥ 0,25 e Ha: p < 0,25
Ho: p = 0,25 e Ha: p ≠ 0,25
Ho: p ≤ 0,25 e Ha: p > 0,25
Ho: p > 0,25 e Ha: p ≤ 0,25
Ho: p ≠ 0,25 e Ha: p = 0,25
Considere o seguinte teste de hipóteses:
Ho: µ ≥ 25
Ha: µ < 25
Uma amostra com 100 elementos é extraída da população e fornece a média igual a 22 e o desvio padrão igual a 12. Para alfa igual a 5%, qual sua conclusão?
Dados adicionais:
Valor de Zcrítico = - 1,645.
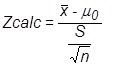
Não rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula porque Zcalc = 3,5 é maior que Z crítico.
Não rejeitar a hipótese nula, porque Zcalc = 2,5 é maior que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 3,5, é menor que Z crítico.
ENADE 2006 Adaptado.
A tabela abaixo mostra como se distribui o tipo de ocupação dos jovens de 16 a 24 anos que trabalham em 5 Regiões Metropolitanas e no Distrito Federal.

Das regiões estudadas, aquela que apresenta o maior percentual de jovens com carteira assinada, dentre os jovens que são assalariados do setor privado, é
Belo Horizonte.
Recife.
Porto Alegre.
Distrito Federal.
São Paulo.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 1,23%
± 5,23%
± 2,23%
± 4,23%
± 3,23%
O controlador de qualidade de certa empresa, desejando estimar a porcentagem de defeitos da linha de produção do produto A, examinou uma amostra de 1000 peças e encontrou 30 defeituosas. Com uma confiança de 95%, qual a porcentagem de peças defeituosas da linha de produção do produto A? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z = 1,96.

3,0%±3,36%.
3,0%± 0,05%.
3,0%±2,54%.
3,0%±2,84%.
3,0%±1,06%.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido e a amostra é grande, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O estagiário errou ao escolher a distribuição de probabilidades Z. Dado que o desvio padrão populacional é desconhecido e a amostra é pequena, deveria ter usado a distribuição t, de Student, na construção do intervalo de confiança.
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido, mas a população de onde provém a amostra é normal, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O estagiário fez a escolha certa. Dado que o desvio padrão populacional é desconhecido e a amostra é pequena, deve ser usada a distribuição normal padronizada Z na construção do intervalo de confiança.
O procedimento do estagiário está correto. Como a amostra provém de uma população normal, é indiferente o uso da distribuição normal padronizada Z ou da distribuição t, de Student.
Uma nova série de televisão precisa provar que tem mais do que 25% da audiência de telespectadores depois das 13 primeiras semanas de exibição para ser julgada bem sucedida. Quais as hipóteses nula (Ho) e alternativa (Ha) adequadas para testar se a série tem mais do que 25% da audiência de telespectadores depois das 13 primeiras semanas de exibição?
Ho: p ≥ 0,25 e Ha: p < 0,25
Ho: p = 0,25 e Ha: p ≠ 0,25
Ho: p ≤ 0,25 e Ha: p > 0,25
Ho: p > 0,25 e Ha: p ≤ 0,25
Ho: p ≠ 0,25 e Ha: p = 0,25
Considere o seguinte teste de hipóteses:
Ho: µ ≥ 25
Ha: µ < 25
Uma amostra com 100 elementos é extraída da população e fornece a média igual a 22 e o desvio padrão igual a 12. Para alfa igual a 5%, qual sua conclusão?
Dados adicionais:
Valor de Zcrítico = - 1,645.
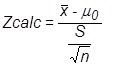
Não rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula porque Zcalc = 3,5 é maior que Z crítico.
Não rejeitar a hipótese nula, porque Zcalc = 2,5 é maior que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 3,5, é menor que Z crítico.
ENADE 2006 Adaptado.
A tabela abaixo mostra como se distribui o tipo de ocupação dos jovens de 16 a 24 anos que trabalham em 5 Regiões Metropolitanas e no Distrito Federal.

Das regiões estudadas, aquela que apresenta o maior percentual de jovens com carteira assinada, dentre os jovens que são assalariados do setor privado, é
Belo Horizonte.
Recife.
Porto Alegre.
Distrito Federal.
São Paulo.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 1,23%
± 5,23%
± 2,23%
± 4,23%
± 3,23%
O controlador de qualidade de certa empresa, desejando estimar a porcentagem de defeitos da linha de produção do produto A, examinou uma amostra de 1000 peças e encontrou 30 defeituosas. Com uma confiança de 95%, qual a porcentagem de peças defeituosas da linha de produção do produto A? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z = 1,96.

3,0%±3,36%.
3,0%± 0,05%.
3,0%±2,54%.
3,0%±2,84%.
3,0%±1,06%.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
Ho: p ≥ 0,25 e Ha: p < 0,25
Ho: p = 0,25 e Ha: p ≠ 0,25
Ho: p ≤ 0,25 e Ha: p > 0,25
Ho: p > 0,25 e Ha: p ≤ 0,25
Ho: p ≠ 0,25 e Ha: p = 0,25
Considere o seguinte teste de hipóteses:
Ho: µ ≥ 25
Ha: µ < 25
Uma amostra com 100 elementos é extraída da população e fornece a média igual a 22 e o desvio padrão igual a 12. Para alfa igual a 5%, qual sua conclusão?
Dados adicionais:
Valor de Zcrítico = - 1,645.
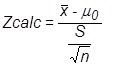
Não rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula porque Zcalc = 3,5 é maior que Z crítico.
Não rejeitar a hipótese nula, porque Zcalc = 2,5 é maior que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 3,5, é menor que Z crítico.
ENADE 2006 Adaptado.
A tabela abaixo mostra como se distribui o tipo de ocupação dos jovens de 16 a 24 anos que trabalham em 5 Regiões Metropolitanas e no Distrito Federal.

Das regiões estudadas, aquela que apresenta o maior percentual de jovens com carteira assinada, dentre os jovens que são assalariados do setor privado, é
Belo Horizonte.
Recife.
Porto Alegre.
Distrito Federal.
São Paulo.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 1,23%
± 5,23%
± 2,23%
± 4,23%
± 3,23%
O controlador de qualidade de certa empresa, desejando estimar a porcentagem de defeitos da linha de produção do produto A, examinou uma amostra de 1000 peças e encontrou 30 defeituosas. Com uma confiança de 95%, qual a porcentagem de peças defeituosas da linha de produção do produto A? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z = 1,96.

3,0%±3,36%.
3,0%± 0,05%.
3,0%±2,54%.
3,0%±2,84%.
3,0%±1,06%.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
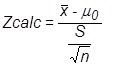
Não rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 2,5 é menor que Z crítico.
Rejeitar a hipótese nula porque Zcalc = 3,5 é maior que Z crítico.
Não rejeitar a hipótese nula, porque Zcalc = 2,5 é maior que Z crítico.
Rejeitar a hipótese nula, porque Zcalc = - 3,5, é menor que Z crítico.
ENADE 2006 Adaptado.
A tabela abaixo mostra como se distribui o tipo de ocupação dos jovens de 16 a 24 anos que trabalham em 5 Regiões Metropolitanas e no Distrito Federal.

Das regiões estudadas, aquela que apresenta o maior percentual de jovens com carteira assinada, dentre os jovens que são assalariados do setor privado, é
Belo Horizonte.
Recife.
Porto Alegre.
Distrito Federal.
São Paulo.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 1,23%
± 5,23%
± 2,23%
± 4,23%
± 3,23%
O controlador de qualidade de certa empresa, desejando estimar a porcentagem de defeitos da linha de produção do produto A, examinou uma amostra de 1000 peças e encontrou 30 defeituosas. Com uma confiança de 95%, qual a porcentagem de peças defeituosas da linha de produção do produto A? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z = 1,96.

3,0%±3,36%.
3,0%± 0,05%.
3,0%±2,54%.
3,0%±2,84%.
3,0%±1,06%.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
Belo Horizonte.
Recife.
Porto Alegre.
Distrito Federal.
São Paulo.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 1,23%
± 5,23%
± 2,23%
± 4,23%
± 3,23%
O controlador de qualidade de certa empresa, desejando estimar a porcentagem de defeitos da linha de produção do produto A, examinou uma amostra de 1000 peças e encontrou 30 defeituosas. Com uma confiança de 95%, qual a porcentagem de peças defeituosas da linha de produção do produto A? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z = 1,96.

3,0%±3,36%.
3,0%± 0,05%.
3,0%±2,54%.
3,0%±2,84%.
3,0%±1,06%.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:

± 1,23%
± 5,23%
± 2,23%
± 4,23%
± 3,23%
O controlador de qualidade de certa empresa, desejando estimar a porcentagem de defeitos da linha de produção do produto A, examinou uma amostra de 1000 peças e encontrou 30 defeituosas. Com uma confiança de 95%, qual a porcentagem de peças defeituosas da linha de produção do produto A? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z = 1,96.

3,0%±3,36%.
3,0%± 0,05%.
3,0%±2,54%.
3,0%±2,84%.
3,0%±1,06%.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:

3,0%±3,36%.
3,0%± 0,05%.
3,0%±2,54%.
3,0%±2,84%.
3,0%±1,06%.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:

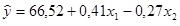 .
.